-
Gesamte Inhalte
2029 -
Benutzer seit
-
Letzter Besuch
-

Welche TrixBrix R40 Weiche ist die richtige?
Henry antwortete auf gleisplaners Thema in Fragen zur Planung
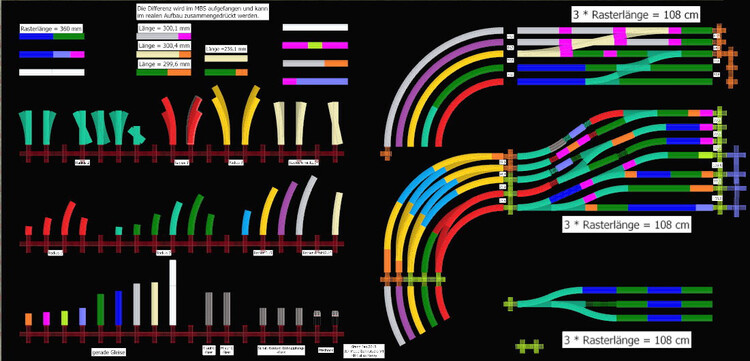
Siehe auch meine Gleissystem-Anlage mit Weichen/Längen- Kombinationen, ID F4ACBB37-6A15-454A-9635-09A7CEA9FBF6 daraus geht hervor, was zusammen passt, meint Henry -

Welche TrixBrix R40 Weiche ist die richtige?
Henry antwortete auf gleisplaners Thema in Fragen zur Planung
@Matze hat die TrixBrix-Weichen hochgeladen. Er kann dir Genaueres sagen, unter welchen "Gleisumständen" die Weiche eingebaut bzw. weitergeführt wird. Ein Gleisbild wäre hilfreich gewesen, grüßt Henry -
Hallo @martin852 kommt nur das starre aber einfache Märklin C-Gleis in Frage. Allerdings gibt es kein Flexgleis. Ich habe eine Beispiel-Anlage mit den möglichen Gleisverbindunden im Online-Katalog abgelegt: FFB08E34-8EAC-4038-9524-E62FD19BAD29 man sollte sich mit der Gleisgeometrie vertraut machen, jedes Gleis hat seinen Sinn, meint Henry
-

Naheliegende Fehlbedienungsmöglichkeit bei Track contact / Connection
Henry antwortete auf Phrontistess Thema in Technischer Support
Sieht es vergleichsweise im deutschsprachigen Menü anders aus (könnte anders "ausgedrückt/übersetzt/interpretiert" worden sein), fragt müde Henry -
Hallo @AndreasWB, ich gebe dir recht --- aber Es ist nicht Aufgabe eines Planungsprogrammes, die Schienen einer Weiche getreu der Bauweise des Herstellers abzubilden, sondern mit den veröffentlichten Konstruktionsmaßen dafür zu sorgen, daß die Gleisanschlüsse korrekt im Gleissystem umgesetzt werden können. Aus Länge, Radius und Winkel kommt im MBS nichts anderes heraus, damit Einbaulage und Gleisabstand eingehalten werden. Du kannst dir natürlich eine eigene Konstruktion wählen, meint Henry P.S.: Ich konnte mir deinen Entwurf nicht zu Gemüte führen und ansehen, weil ich vom Forum z.Z. nichts downloaden kann. Viellecht per Mail im Forum ?
-
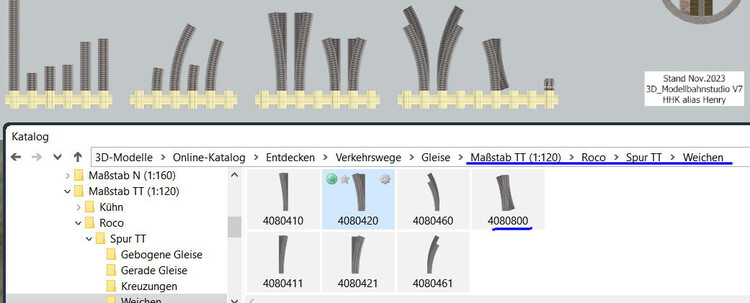
Hallo @AndreasWB, Danke für den Hinweis, den nachfolgende Anwender nützlich finden werden, aber diesmal war ich schneller , Roco TT ist im MBS enthalten. Kühn bleibt erhalten, Roco TT ist neu. Viele Grüße von Henry
-
Hallo allerseits, neuerdings läßt Norton nach einem update keine Downloads aus dem Forum mehr zu und meldet; Weiß jemand , an welcher Einstellung ich in Norton drehen muß, um wie vorher Dateien herunter zu laden ? Viele Grüße von Henry
-

Onlinekatalog - Spur 2 1:22,5 - Thiel Gleise - Skalierungsproblem
Henry antwortete auf oefferlberns Thema in Feature-Wünsche
Hallo @oefferlbern das erklärt schon mal was. Ich hatte das System mal renoviert, aber vergessen, die Änderungen hochzuladen. Allerdings gab es auch keine Rückmeldungen der Benutzer. Weil sich aber die Bestellnummern geändert haben, nehme ich dies zum Anlass, das Thiel IIm Gleissystem neu aufzulegen, damit die Gartenbahn unterm Weihnachtsbaum ihre Probefahrt absolvieren kann. Danke für den Hinweis sagt Henry -

Onlinekatalog - Spur 2 1:22,5 - Thiel Gleise - Skalierungsproblem
Henry antwortete auf oefferlberns Thema in Feature-Wünsche
Hallo @oefferlbern ich schaue es mir an. Es wäre aber hilfreich, wenn du deine Beispieldatei mit hochladen würdest, HG, Henry -
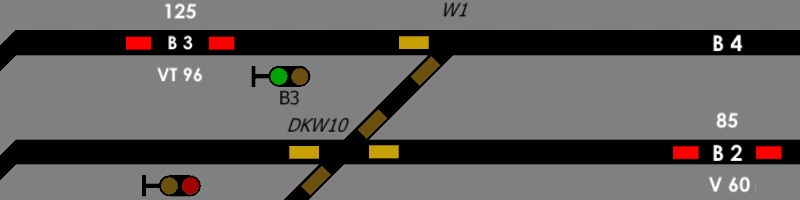
Moin, nur vorsichtshalber sei vermerkt, daß es nicht darauf ankommt, welche Schaltpositionen verwendet werden, sondern daß sie gleichbleibend bezeichnet sein müssen. Möglicherweise spielt auch die Anzahl der Schaltmöglichkeiten je Signal eine Rolle. Formsignale haben maximal 3 - Lichtsignale mehr Schaltstellungen. Das könnte Nebeneffekte haben, meint Henry
-

Zielgenauigkeit bei Objektauswahl via Maus-Klick erhöhen.
Henry antwortete auf Eggus Thema in Technischer Support
dann mach es doch , meint Henry -
Hallo, ich habe soeben zum Lemiso Spur T das Roco Spur TT Gleissystem hochgeladen. Nach Freigabe durch Neo stehen sie Euch zur Verfügung. Viele Grüße, Henry P.S.: Beispielanlagen sind in Arbeit.
-
Hallo zusammen, ich habe eben das Lemiso Spur T Gleissystem hochgeladen. Nach Freigabe durch Neo steht es Euch zur Verfügung. Viele Grüße, Henry
-
Hallo @Gerald23 ich habe die Lemiso Gleise bereits fertig gestellt und warte auf die Bereitstellung der Kategorien, um sie hochzuladen. Um noch etwas Geduld, bittet Henry
-
Hallo, leider wurde die Spurmaßstabzahl mit 480 falsch angegeben, der Maßstab der Spur T ist 1 : 450 Es gibt jedoch einen lokalen Hersteller für die Spur QTT im Maßstab 1 : 480, der aber auch die 3mm breiten Gleise verwendet. Man lernt nicht aus, grüßt Henry Ich kümmere mich um die Lemiso Gleise.

t.thumb.jpg.9a65b36ee1f1ca7b15469c48306c1c11.jpg)